Cryptographic history can be viewed as a running battle between the code makers and the code breakers, and as Part I concluded, the code makers were winning. The polyalphabetic Vigenère cipher proved impregnable for 300 years. In the mid 19th century a British dentist and amateur crytographer, ignorant of cryptographic history, independently reinvented the cipher and issued a public challenge to break it. This annoyed Charles Babbage sufficiently to do so.
Babbage, an all-around great scientist who invented the “difference engine,” a forerunner of the modern computer, used to solve the ciphers in the newspapers’ “agony columns” for fun, which possibly inspired him to the wisest remark in the history of cryptography: “very few ciphers are worth the trouble of unravelling them.” To solve the Vigenère cipher he employed no arcane mathematics, just common sense. He reasoned that the Vigenère cipher is simply a series of monoalphabetic substitution ciphers, repeating every n letters, n being the length of the keyword. The first question is, how long is the keyword?
Babbage looked for repeating sequences in the ciphertext, reasoning that the distance between these sequences will be a multiple of the length of the keyword; i.e., that these sequences encipher the same plaintext. If, say, a four-letter sequence shows up twice in a Vigenère ciphertext, the probability that it represents two different plaintexts is vanishingly small. Babbage then counted the number of letters between the various repeated sequences, and solved for the common factors. Suppose you have a ciphertext with a four-letter sequence repeated 98 letters apart, and a five-letter sequence repeated 35 letters apart. The keyword will be seven letters long.
Once you find the length of the keyword, you’ve reduced the problem to solving seven separate monoalphabetic substitution ciphers. You resort to standard frequency analysis, and you’re done. Babbage essentially decomposed the problem, breaking it into two separately manageable chunks.
All of this time the code makers had not stood still. They developed more and more difficult polyalphabetic ciphers, culminating in Arthur Scherbius’ invention in 1918 of the notorious Enigma machine. Enigma was essentially a triple-shifting device; here’s a partial schematic:
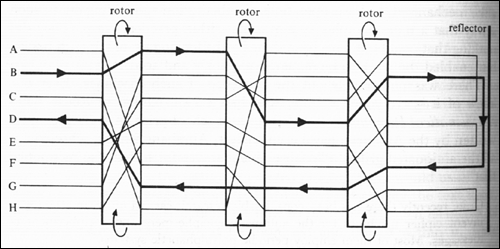
The input device was a typewriter keyboard; the output device was a lampboard of the alphabet above it. Each of three rotors, or scramblers, acted as a monoalphabetic substitution cipher. When the operator typed a letter, it would pass through a first scrambler, which would shift it according to its setting, and then rotate one place. The second scrambler would shift it again, and rotate one place itself, after the first scrambler had made a complete rotation of 26 places. Same deal with the third scrambler. Finally the letter would be bounced off a reflector, pass back through the three rotors in reverse order, and the ciphertext — or plaintext, if you were decrypting — letter would light up on the lampboard. To compound the nastiness, the machine included a plugboard, which allowed arbitrary pairs of letters to be swapped before entering the three scramblers. The key consisted of the plugboard settings, the order of the three scramblers, and their initial settings.
Everyone knows that Enigma was broken by British cryptographers, principally Alan Turing, at Bletchley Park during the Second World War. Everyone is wrong. It was actually a Polish cryptographer, Marian Rejewski, who broke Enigma in 1932. The math is too complicated to go into here (Simon Singh provides a lucid description) but Rejewski found a very clever way to separate the effect of the plugboard from the effect of the scrambler, decomposing the problem, just as Babbage had before him. He also relied on cribs, an essential tool of the cryptographer. A crib is boilerplate plaintext that a cryptographer can expect to find somewhere in a message. Computer file headers, dates and times, and names are all excellent cribs. Rejewski’s crib was the fact that the Germans, when transmitting the daily key, would repeat it to deal with possible radio interference. This, and his genius, were enough for him to break Enigma.
This is not to slight the achievements of Alan Turing and his Bletchley colleagues. The Germans eventually stopped transmitting the key twice, depriving Rejewski of his crib. They increased the number of letter pairs swapped in the plugboard from six to ten. And they added two more scramblers, so there were 60 possible scrambler orders instead of only 6. By 1938 the Poles could no longer decipher Enigma messages, and the intelligence blackout was not lifted until Turing and the Bletchley Park cryptanalysts, again using decomposition techniques, broke the more complicated version in August 1940. (A good history of Enigma can be found here. You can try it yourself on this virtual Enigma machine.)
With the advent of computers in the 1950s and 1960s encryption techniques began to be freed of hardware limitations. The Enigma machine was bulky and complex, but an Enigma program is trivial, and increasingly complex algorithms were tried. The best of them was called Lucifer, developed by Horst Feistel for IBM. Lucifer relies, like Enigma, on a combination of transposition and substitution. (In the end, as in the beginning, are transposition and substitution.) But it’s orders of magnitude more complex. Lucifer, like most modern cryptographic algorithms, is a block cipher: it translates messages into binary digits, breaks them into blocks of 64, and encrypts them one at a time, using a series of 16 “rounds.” Simon Singh compares the process to kneading dough.
The U.S. government adopted Lucifer in 1976 as its official encryption standard, prosaically renaming it DES (Data Encryption Standard). It remained the standard algorithm until three years ago, when it was replaced by Rijndael (pronounced, approximately, Rhine-doll). DES is still theoretically unassailable. Its weakness lies not with the algorithm itself but the fact that the key, 56 bits, is too short; computers are now barely fast enough to check all the possibilities. Many experts suspect that the National Security Agency insisted on a 56-bit key because it didn’t want to endorse an algorithm it couldn’t break itself. (Update: My father, who was there, denies this story, and provides an authoritative account in the comments.)
OK, now we have an unbreakable algorithm. We can pack our bags and go home, right? Not so fast. There remains the problem of key distribution. If you and I want to encrypt our messages, we still need to share a secret, the encryption key. We can meet to agree on it, or I can send it to you by FedEx or carrier pigeon, but even with only two parties involved the logistical difficulties are considerable.
Cryptographers had always assumed that ciphers required a shared secret. Two Stanford researchers, Martin Hellman and Whitfield Diffie, asked themselves why this should be so. Diffie and Hellman wanted to know if it was possible for two strangers, with no previous agreements, to encrypt securely to each other.
Remarkably enough, they discovered, after a few years of dead ends, a way to do this simple enough to demonstrate on the back of a bar napkin. Suppose Alice and Bob — in the literature it’s always Alice and Bob — want to agree on a secret, which they will use as a key to encrypt subsequent messages. First Alice and Bob agree on two numbers, an exponent base, Y, and a modulus, P. We’ll choose small numbers, Y=5 and P=7, to keep it simple. They exchange these numbers openly. Next Alice and Bob each choose a secret number, call it X. Say Alice chooses 4 and Bob chooses 2. They keep these to themselves. Now they each calculate the following:
YX (mod P)
In other words, raise Y to the exponent X, divide the result by P, and take the remainder, which we’ll call Z. Alice’s result is 54 (mod 7) = 625 (mod 7) = 2, she sends to Bob. Bob’s result is 52 (mod 7) = 25 (mod 7) = 4, which he sends to Alice. Now Alice and Bob both take each other’s result and plug it into the following formula:
ZX (mod P)
For Bob, this is 22 (mod 7) = 4. For Alice, this is 44 (mod 7) = 256 (mod 7) = 4. Alice and Bob have ended up with the same number! This number is the encryption key. Of course in real life Alice and Bob would use extremely large numbers for P, Y, and X, and they would end up with an extremely large number for a key. But the amazing part is that it is impossible to deduce the key from the information that Alice and Bob exchange. Starting from zero, they now have a shared secret, and can encrypt to their heart’s content. For my money this is the greatest breakthrough in the history of cryptography.
There is one crucial limitation to Diffie-Hellman key exchange: it requires both parties to be present. It works for synchronous but not asynchronous communication. Unfortunately, the most common form of electronic communication, email, is asynchronous. Diffie set himself this problem. Until now all cryptographic systems had relied on a single key, and decryption was simply the reverse of encryption. Diffie wondered, again, why this must be. Suppose you had separate keys for encryption and decryption, and that it was impossible to deduce one key from the other. Then the encryption key could be public — in fact, you would want it to be widely publicized. Then if Alice wants to send Bob an encrypted message, she looks up Bob’s public key in a directory, encrypts the message, and sends it to Bob. Bob receives the message later and decrypts it, using his private key, at his leisure. Diffie had stumbled on the concept of public-key cryptography.
But only the concept: he still needed an implementation. This was finally supplied in 1977 by two MIT computer scientists, Ron Rivest and Adi Shamir, and a mathematician, Leonard Adleman. RSA is remarkably simple, only slightly more complicated than Diffie-Hellman key exchange, and although other public-key algorithms have since been discovered, RSA is still the principal one in use. Rivest, Shamir, and Adleman founded a company on its strength, RSA Security, and have grown very rich. (It was revealed, many years later, that three British cryptanalysts, James Ellis, Clifford Cocks, and Malcolm Williamson, working for the British government, had independently discovered key exchange and public-key cryptography years before Diffie, Hellman, and Rivest and company, but the government refused to release their findings. Don’t work for the government if you want to be rich and famous.)
RSA relies for its secrecy on the difficulty of factoring very large numbers. Most mathematicians believe that factorization is what they call, with their usual flair for terminology, a “hard” problem, meaning that it can’t be solved significantly faster than by trying all the possibilities. If they’re right, RSA will never be broken, and the history of cryptography is effectively at an end. The code makers have won, this time for good.
Sources
The Code Book by Simon Singh is an excellent, very readable overview of the history of encryption, including a cipher contest, consisting of 10 encrypted messages, ranging from the simple to the insanely difficult, with a prize of $15,000 to the first person to solve them all. Too late: a Swedish team already won.
The Codebreakers by David Kahn is the definitive history, ending at the mid-1960s, right before Diffie-Hellman and RSA. At 1100 pages, it requires considerable ambition. Whit Diffie, while he was dreaming up Diffie-Hellman key exchange and public-key cryptography, carried a copy around with him for years, which must have been awkward, since the book is nearly as tall as he is.
Applied Cryptography by Bruce Schneier. Comprehensive descriptions and source code for all major modern algorithms.